集合A,Bがそれぞれあったとき、
「AかつBでない」は「Aでない、またはBでない」に等しい。
「AまたはBでない」は「Aでない、かつBでない」に等しい。
これだけだとよくわからないですね。図で見ると少しわかりかもしれません。こちらで確認してみてください。 日本語で例を見てみるともっとわかりやすいとかもしれません。 例えば 「彼女は学生かつ男子でない」は言い換えれば「彼女は学生でない、または男子でない」ということになります。 はい。自分で書いてて全然ピンとこないです。言い換えたあとの文章に意味があるのか?と疑問が浮かびます。 多分これが「何に使えんの?」っていう疑問につながってるんじゃないかと思います。 さて、ここで本題のこれがコンピュータの何に使われているのかですが、なんとド・モルガンの法則、コンピュータの基本構成最小単位、論理回路にも適用できるのです!
すごいことなんですが、論理回路がわかないと意味がわからないので、ちゃんと解説していきます。 具体的な使い方を見ていきましょう。まず論理回路とは [caption id="" align="alignnone" width="539"] Logic Circuit[/caption]
こんな感じのものです。一度は皆さんも見たことがあると思います。
これらは電子回路で、例えばNOT回路のAに電気が流れてくるとĀには電気は流れません。
逆にAに電気が流れて来ないとき、Āには電気を流します。
AND回路はAとB(つまりA and B)のどちらもに電気が流れてきたときABに電気が流れていき、
そうでないときはABに電気は流れません。OR回路もその名の通り、AとBどちらか(A or B)に電気が流ればその先に電気が流れます。
このように条件によって電気の流れる、流れないを管理している電子回路を論理回路というのですが、
なんとコンピュータはこれの組み合わせによって作られています。
みなさんがこのページを見ているパソコン、スマホももちろんそうです。
そして、ここからが肝ですが、この論理回路にド・モルガンの法則が適用できるのです。
「かつ」はAND回路、「または」はOR回路、「ない(否定)」はNOT回路に対応していますので、
例えば AND回路にNOT回路を組み合わせたNAND回路は
Logic Circuit[/caption]
こんな感じのものです。一度は皆さんも見たことがあると思います。
これらは電子回路で、例えばNOT回路のAに電気が流れてくるとĀには電気は流れません。
逆にAに電気が流れて来ないとき、Āには電気を流します。
AND回路はAとB(つまりA and B)のどちらもに電気が流れてきたときABに電気が流れていき、
そうでないときはABに電気は流れません。OR回路もその名の通り、AとBどちらか(A or B)に電気が流ればその先に電気が流れます。
このように条件によって電気の流れる、流れないを管理している電子回路を論理回路というのですが、
なんとコンピュータはこれの組み合わせによって作られています。
みなさんがこのページを見ているパソコン、スマホももちろんそうです。
そして、ここからが肝ですが、この論理回路にド・モルガンの法則が適用できるのです。
「かつ」はAND回路、「または」はOR回路、「ない(否定)」はNOT回路に対応していますので、
例えば AND回路にNOT回路を組み合わせたNAND回路は
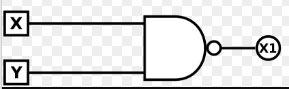 このような回路になります(◯はNOT回路を表しています)。「X1はXかつYでない」と論理的に表現できますが、
ド・モルガンの法則では「X1はXかつYでない」と言うのは「X1はXでないまたはYでない」と言い換えることができるので、NAND回路は
このような回路になります(◯はNOT回路を表しています)。「X1はXかつYでない」と論理的に表現できますが、
ド・モルガンの法則では「X1はXかつYでない」と言うのは「X1はXでないまたはYでない」と言い換えることができるので、NAND回路は
 この回路と同じことになります。上と下は全く同じ動作を行います。
つまり、ド・モルガンの法則によって回路の節約、そして違う回路の作成ができるようになります。
下は3つの回路を使っているのに、それを上で表現することで2つの回路で済ませたり、
AND回路がないとき、OR回路とNOT回路はあるのに・・・というときでも、NAND回路をつかうことなどができるのです。
さらに、ド・モルガンの法則を使うことによってNAND回路のみの組み合わせで他の論理回路すべてを表現することができます。
言い換えれば、NAND回路一種類の組み合わせによって、コンピュータが成り立っているといえます。すごごごいよー!!
わかりましたでしょうか?
ド・モルガンの法則は一見使いみちがないように思えますが、誰もが使っているコンピュータでふんだんに使われていたのです。
ド・モルガンの法則のに触れていないのは恐らく、生まれたばかりの赤ちゃんくらいのものでしょう。それ以外の人はみんなド・モルガンの法則に助けられていると言っても過言ではありません。
ということで、ここまで偉大な法則を教えないわけにはいかないでしょうが、ここまで専門的な問題を数学の試験に取り込むわけにもいきません。ド・モルガンの法則にはこのような背景があったのです。
よく見るベン図に対する皆さんの気持ちも、少しは変わったのではないでしょうか。
以上、明日ロシア語の試験を控えながら、2時間ほどかけてブログ記事を書いて、かなり焦っている学生講師の川上の記事でした。
もっと気になる人はNAND回路からテトリスを作るまでを、実際に手を動かしながら学べる本がありますので、ぜひ読んでみてください。自分も途中まで進めていますが、とっても楽しいです。ワクワクしながら学べます。
[amazon_link asins=’4873117127′ template=’ProductLink’ store=’atarasi09-22′ marketplace=’JP’ link_id=’112344ae-0462-11e8-acbe-b16a52ca028d’]]]>
この回路と同じことになります。上と下は全く同じ動作を行います。
つまり、ド・モルガンの法則によって回路の節約、そして違う回路の作成ができるようになります。
下は3つの回路を使っているのに、それを上で表現することで2つの回路で済ませたり、
AND回路がないとき、OR回路とNOT回路はあるのに・・・というときでも、NAND回路をつかうことなどができるのです。
さらに、ド・モルガンの法則を使うことによってNAND回路のみの組み合わせで他の論理回路すべてを表現することができます。
言い換えれば、NAND回路一種類の組み合わせによって、コンピュータが成り立っているといえます。すごごごいよー!!
わかりましたでしょうか?
ド・モルガンの法則は一見使いみちがないように思えますが、誰もが使っているコンピュータでふんだんに使われていたのです。
ド・モルガンの法則のに触れていないのは恐らく、生まれたばかりの赤ちゃんくらいのものでしょう。それ以外の人はみんなド・モルガンの法則に助けられていると言っても過言ではありません。
ということで、ここまで偉大な法則を教えないわけにはいかないでしょうが、ここまで専門的な問題を数学の試験に取り込むわけにもいきません。ド・モルガンの法則にはこのような背景があったのです。
よく見るベン図に対する皆さんの気持ちも、少しは変わったのではないでしょうか。
以上、明日ロシア語の試験を控えながら、2時間ほどかけてブログ記事を書いて、かなり焦っている学生講師の川上の記事でした。
もっと気になる人はNAND回路からテトリスを作るまでを、実際に手を動かしながら学べる本がありますので、ぜひ読んでみてください。自分も途中まで進めていますが、とっても楽しいです。ワクワクしながら学べます。
[amazon_link asins=’4873117127′ template=’ProductLink’ store=’atarasi09-22′ marketplace=’JP’ link_id=’112344ae-0462-11e8-acbe-b16a52ca028d’]]]>